Pariul pe egalitate la baccarat (tie bet) permite jucătorului să parieze că rezultatul următoarei mâini va fi egalitate între mâinile Jucătorului și Bancherului. Acest pariu este o parte standard a jocului, așa cum este, de exemplu, asigurarea la blackjack. Dorința de a număra cărțile în jocul principal de baccarat este cunoscută încă de la studiile cunoscutului Dr. Ed Thorp care scria în cartea sa Beat the Dealer - „Nu există nicio strategie perfectă pentru a câștiga în jocul din Nevada, chiar și dacă ai avea un computer care să joace perfect”. Am abordat numărarea cărților la baccarat de numărare a cărților în alte postări din blogul 888casino. Din câte îmi pot da seama, nu s-a făcut nicio încercare serioasă de a studia jocul perfect computerizat sau numărarea cărților împotriva Tie Bet. Acest material vine să corecteze acest deficit din literatură.
Există două tabele comune de plată pentru pariul pe egalitate la baccarat, unul plătind 8 la 1, iar celălalt plătind 9 la 1. În mod surprinzător, cazinourile au descoperit că pariul Tie este jucat mai des cu o plată de 8 la 1, deoarece mulți asiatici cred că „8” este un număr norocos. Următoarele tabele oferă analiza combinatorie pentru pariul pe egalitatea la jocul baccarat:

Versiunea cu plată 8-1 oferă casei o marjă de profit de 14,360%, iar versiunea 9-1 o marjă de 4,844%.
Pariul Tie a fost analizat pentru jocul avantajos de autorul John May, care a scris despre descoperirile sale în cartea sa: „Baccarat for the Clueless.” Metoda lui implică un joc spre final. Atunci când cărțile rămase în suport (obiectul în care se țin cărțile de joc pe masă), sunt predominant egale (cărți cu valorile 0, 2, 4, 6, 8), sunt mai multe șanse să rezulte un număr par, deoarece suma a două numere pare este mereu un număr par. Într-un articol, el susține că jucătorul poate câștiga 0,00504 unități per suport cu o frecvență a pariului de 0,01% (o dată la 10.000 de mâini) și un avantaj mediu de 62%. Nu am de gând să-i verific munca, dar niciun AP (Advantage Player - jucător care caută vulnerabilități în jocurile de cazino) serios nu ar încerca să profite de o astfel de oportunitate.
Astfel, voi lua în considerare mai întâi versiunea 8-1. Pentru a înțelege potențialul său, am efectuat o simulare a 100.000 de suporturi. Pentru fiecare suport, am calculat marja casei/jucătorului în momentul în care mai erau 26 de cărți rămase în suport. Iată rezultatele:

Axa orizontală prezintă avantajul casei/jucătorului. Axa verticală indică probabilitatea ca marja să apară. Partea distribuției din dreapta liniei verticale portocalii corespunde potențialului de profit pentru AP. Frecvența jucătorului care are o marjă de profit este pur și simplu aria de sub curba din dreapta liniei verticale. Marja medie este media ponderată (punctul de echilibru) a porțiunii de sub curba din dreapta liniei verticale.
Pentru a fi mai specific, cu 26 de cărți rămase în joc:
- Jucătorul va avea avantaj la 1,89% din suporturi.
- Marja medie a jucătorului (atunci când o are) este de 4,62%.
Cu toate acestea, aceste numere nu înseamnă că 8-1 nu poate fi învins în circumstanțele potrivite. Un jucător a spunea odată că a găsit un joc online în care în ultima rundă pot fi împărțite 7 cărți. În această situație, jucătorul poate folosi cu ușurință un program de calculator pentru a determina când să aleagă pariul pe egalitate.
Cu 7 cărți rămase în joc:
- Jucătorul va avea avantaj la 31.41% din suporturi.
- Marja medie a jucătorului (atunci când o are) este de 35.17%.
Iată distribuția:

O aproximare liniară simplă oferă o limită superioară de aproximativ 0,33 unități per suport, folosind jocul perfect computerizat, atunci când într-un joc 8 la 1 sunt împărțite 7 cărți (nevăzute).
Aceste cifre sunt în concordanță cu constatările lui John May. Într-un joc dintr-un cazino terestru cu cartea tăiată plasată la 14 cărți, nu există aproape nimic de remarcat în jocul 8-1. AP urmărește o parte atât de mică din distribuție, în timp ce folosește instrumente imperfecte, încât pariul este în esență imbatabil.
Nu același lucru se poate spune despre versiunea 9-1. În acest caz, există cu siguranță o porțiune considerabilă a distribuției la dreapta liniei verticale portocalii. Efectuând simulări în diferite puncte spre sfârșitul cărților din suport, am estimat pe calculator câștigurile potențiale obținute în urma unui joc perfect. Următorul tabel prezintă distribuția marjelor pentru versiunea 9-1 a pariului pe egalitate, pentru diferite numere de cărți neieșite, de la 18 la 66. Fiecare slide a fost obținut printr-o simulare în baza a 100.000 de suporturi.
Marja medie și frecvența pariurilor pentru fiecare distribuție sunt prezentate în următorul tabel:

Am folosit aceste date pentru a obține o limită superioară absolută a câștigurilor potențiale ce pot fi obținute jucând în avantaj împotriva pariului pe egalitate în varianta 9-1. Deoarece se folosesc cel puțin 4 cărți la o mână, limita superioară se obține prin însumarea valorilor din rândul „unități per suport” și înmulțirea acestei valori cu 2. Astfel, rezultă:
Câștigurile pe pariuri egale per suport ≤ 0,094 unități
Acest lucru ne permite să cuantificăm pe deplin vulnerabilitatea pariului de tip Tie la baccarat. Dacă unei persoane i se permite să folosească un program de calculator pentru a stabili când să parieze pe egalitate și acea persoană mizează 100 USD pe un Tie Bet ori de câte ori are avantaj, atunci jucătorul va câștiga cel mult 9,40 USD per suport.
Următorul pas este să vedem dacă există o modalitate practică (legală) de a obține o parte din acel profit de 9,40 USD per suport. Pentru a face acest lucru, am dezvoltat un sistem de numărare a cărților pe care să îl folosesc la pariurile pe egalitate. Primul pas a fost să iau în considerare efectul de îndepărtare (EOR) pentru fiecare carte. EOR oferă pur și simplu modificarea marjei casei obținută prin îndepărtarea fiecărei cărți din suport și recalculând-o. Coloana finală înmulțește pur și simplu fiecare valoare din coloana EOR cu 3,300. Acest lucru a fost făcut pentru a ajuta la generarea unui sistem rezonabil de numărare a cărților.

Uitându-ne la coloana finală, am investigat sistemul de numărare al cărților cu următoarele etichete:
- A = 0
- 2, 3, 4, 5 = -1
- 6, 7 = -4
- 8, 9, T = 2
Acest sistem de numărare a cărților este destul de inedit pentru jocul de baccarat. Este, de asemenea, non-intuitiv. În încercarea de a înțelege de ce acesta ar trebui să fie sistemul corect de numărare a cărților, m-am gândit cât de des este probabil să apară o egalitate. Mi-a trecut prin minte că avantajul pe care-l putem obține pentru Tie Bet se schimbă în funcție de numărul de cărți cerut de mână. Iată aceste marje:
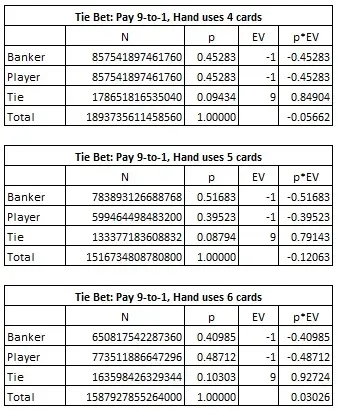
Din aceste calcule, vedem că jucătorul are un avantaj de 3,026% la pariul Tie, dacă știe dinainte că mâna va necesita șase cărți. Cum se potrivește sistemul de numărare a cărților cu etichete (0, -1, -1, -1, -1, -4, -4, 2, 2, 2) cu această observație?
Este clar că 8 și 9 au cele mai mici șanse să apară într-o mână care necesită șase cărți; prin urmare, marja se înclină spre jucător pe măsură ce acele cărți sunt îndepărtate. În același timp, cărțile 6 și 7, atunci când sunt împărțite ca a cincea carte, aproape întotdeauna necesită ca și o a șasea carte să fie extrasă. Prin urmare, aceste cărți favorizează casa pe măsură ce sunt scoase din suport. Suporturile bogate în cărți 6 și 7 și sărace în cărți 8 și 9 duc la o creștere semnificativă a mâinilor care necesită șase cărți.
Am rulat o simulare de o sută de milioane (100.000.000) de suporturi de cărți la baccarat, folosind sistemul de numărare a cărților cu etichete prezentat mai sus (0, -1, -1, -1, -1, -4, -4, 2, 2, 2 ). Cartea tăiată a fost plasată la 14 cărți, ca de obicei. Această simulare a fost pentru tabelul de plată 9-1. Următorul tabel oferă informații statistice obținute în urma acestei simulări:
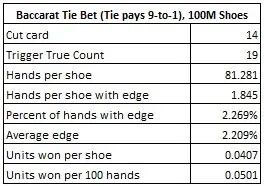
Această simulare arată că AP ar trebui să parieze pe egal ori de câte ori numărătoarea adevărată este +19 sau mai mult. Dacă o face, atunci va face un Tie Bet la 2,269% din mâinile sale, cu un avantaj mediu de 2,209% ori de câte ori face acest pariu pe egalitate. Dacă AP mizează 100 USD pe Tie Bet ori de câte ori numărul atinge limita de declanșare, atunci AP va câștiga aproximativ 4,07 USD per suport.
Câștigurile calculate mai sus, 4,07 USD per suport, reprezintă 43,3% din câștigurile maxime de 9,40 USD per suport disponibile cu un joc perfect computerizat. Abordarea de numărare a cărților nu este deosebit de eficientă, dar este cu mult superioară metodei de joc final sugerată de John May.
Poate cea mai mare barieră în calea jocului în avantaj pe Tie Bet este lipsa disponibilității câștigului 9-1. Am cercetat un număr de cazinouri terestre și nu l-am găsit disponibil nicăieri. Jucătorii preferă să parieze la o marjă mai mare a casei, 8-1, considerată mai „norocoasă” grație numărului 8. Cu toate acestea, poți găsi multe mese de baccarat online la care se plătește 9-1, ceea ce creează o oportunitate unică pentru un AP sau jucător care folosește jocul perfect pentru computer.
Cea mai sigură protecție din partea cazinoului este să continue pur și simplu să ofere mese de baccarat cu tabel de plată 8-1. Dacă găsești un cazino cu tabel de plată 9 la 1, urmărește jucătorii care mizează mult pe Tie Bets când cărțile din suport sunt pe terminate. Nu vor câștiga sume prea mari, dar asta nu înseamnă că nu vor urmări acest lucru.


